道格拉斯-普克抽稀算法,是用来对大量冗余的图形数据点进行压缩以提取必要的数据点。
文章包括三部分
算法原理
代码实现(csharp)
实际应用举例对比(图)
道格拉斯普克算法原理 该算法实现抽稀的过程是:
1)对曲线的首末点虚连一条直线,求曲线上所有点与直线的距离,并找出最大距离值dmax,用dmax与事先给定的阈值D相比:
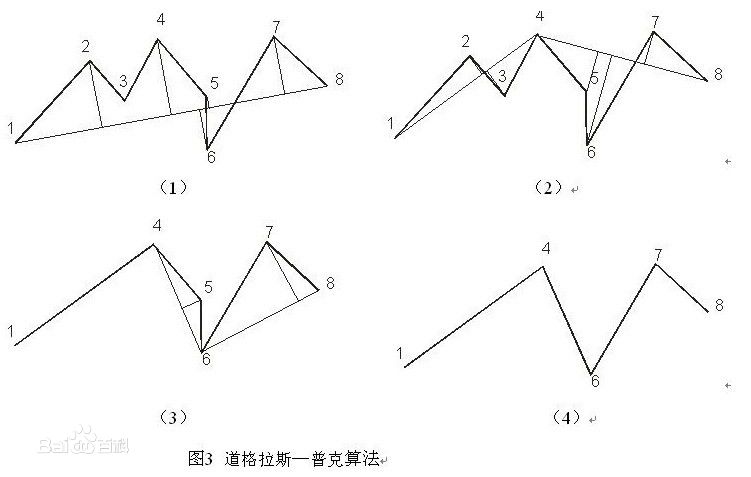
网上找了个示意图:
图一:douglas-peuker 算法示意图 ,来源:百度百科
代码实现 几年前用 c# 封装的一个关于地图的工具包,包含 道格拉斯普克抽稀算法-用于 历史轨迹回放;点面射线算法-用于电子围栏,判断点是否在不规则平面多边形内;各种地图的经纬度纠偏-用于火星坐标和真实坐标的转换(可能存在最近几年地图供应商算法已经改变了);下面给出道格拉斯普克抽稀算法,下一篇说下 平面内判断点在多边形内的射线算法;
坐标对象GeometryModels.cs,包含点,线,多边形的定义
GeometryModels.cs 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 using System;using System.Collections.Generic;using System.Linq;using System.Web;namespace L.MapUtil { public enum TransType { Baidu, Mapbar, Mars } public class GeometryModels { } public class Point { public double X { set ; get ; }public double Y { set ; get ; } public Point (double x, double ythis .X = x; this .Y = y; } public Point ( } public class Line { public Point a { set ; get ; }public Point b { set ; get ; } public Line (Point start, Point end )this .a = start; this .b = end; } } public class Polygon { public List<Line> Plines { get ; set ; } } }
MassPointCompressUtil.cs
MassPointCompressUtil.cs 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 using System;using System.Collections.Generic;namespace L.MapUtil { class MassPointCompressUtil { public static List<Point> MassPointCompress (List<Point> Points, Double Tolerance) { if (Points == null || Points.Count < 3 || Tolerance>0 ) return Points; Int32 firstPoint = 0 ; Int32 lastPoint = Points.Count - 1 ; List<Int32> pointIndexsToKeep = new List<Int32>(); pointIndexsToKeep.Add(firstPoint); pointIndexsToKeep.Add(lastPoint); while (Points[firstPoint].Equals(Points[lastPoint])) { lastPoint--; } DouglasPeuckerReduction(Points, firstPoint, lastPoint, Tolerance, ref pointIndexsToKeep); List<Point> returnPoints = new List<Point>(); pointIndexsToKeep.Sort(); foreach (Int32 index in pointIndexsToKeep) { returnPoints.Add(Points[index]); } return returnPoints; } private static void DouglasPeuckerReduction (List<Point> points, Int32 firstPoint, Int32 lastPoint, Double tolerance, ref List<Int32> pointIndexsToKeep ) Double maxDistance = 0 ; Int32 indexFarthest = 0 ; for (Int32 index = firstPoint; index < lastPoint; index++) { Double distance = PerpendicularDistance (points[firstPoint], points[lastPoint], points[index]); if (distance > maxDistance) { maxDistance = distance; indexFarthest = index; } } if (maxDistance > tolerance && indexFarthest != 0 ) { pointIndexsToKeep.Add(indexFarthest); DouglasPeuckerReduction(points, firstPoint, indexFarthest, tolerance, ref pointIndexsToKeep); DouglasPeuckerReduction(points, indexFarthest, lastPoint, tolerance, ref pointIndexsToKeep); } } private static Double PerpendicularDistance (Point Point1, Point Point2, Point Point) { Double area = Math.Abs(.5 * (Point1.X * Point2.Y + Point2.X * Point.Y + Point.X * Point1.Y - Point2.X * Point1.Y - Point.X * Point2.Y - Point1.X * Point.Y)); Double bottom = Math.Sqrt(Math.Pow(Point1.X - Point2.X, 2 ) + Math.Pow(Point1.Y - Point2.Y, 2 )); Double height = area / bottom * 2 ; return height*100000 ; } } }
实际应用 以前系统10-30秒汇报一次经纬度,所有的点都在地图上绘制,简直反人性化。2012年主导中联GPS应用项目后应用了该算法,目前中联大部分GPS应用相关项目都应用了该算法
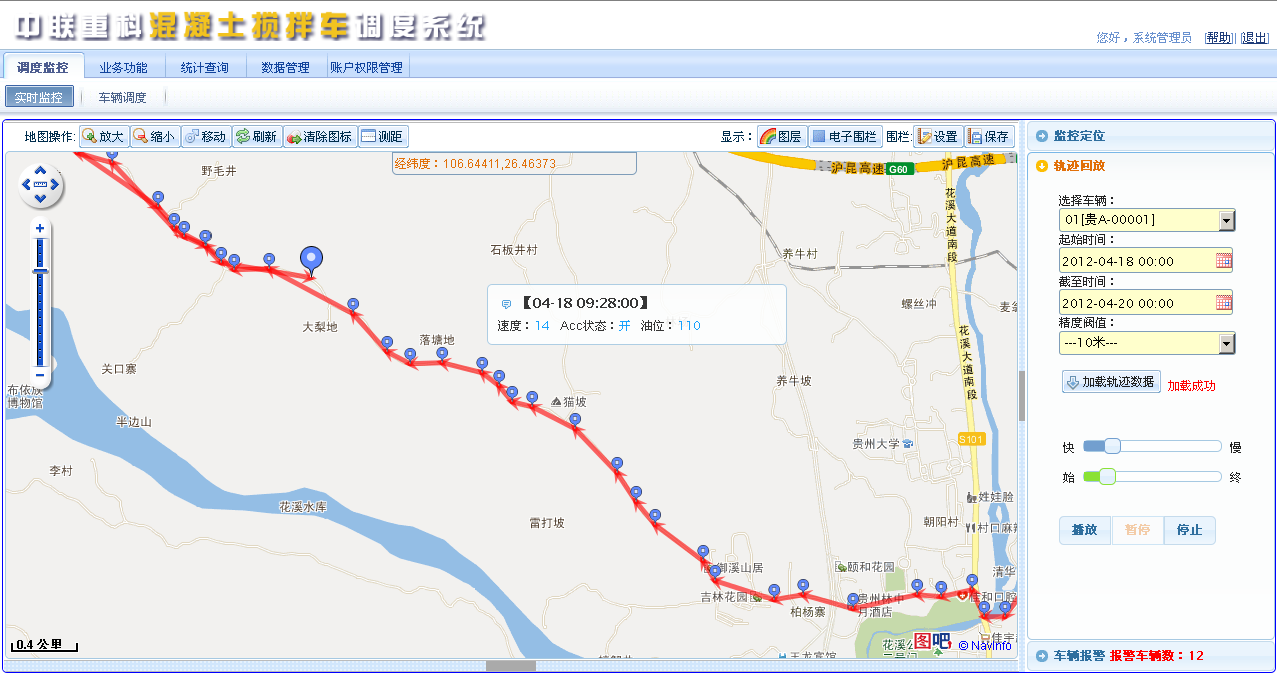
图二:2012年 中联搅拌车调度系统,贵阳某客户搅拌车 轨迹回放 ,10米阀值
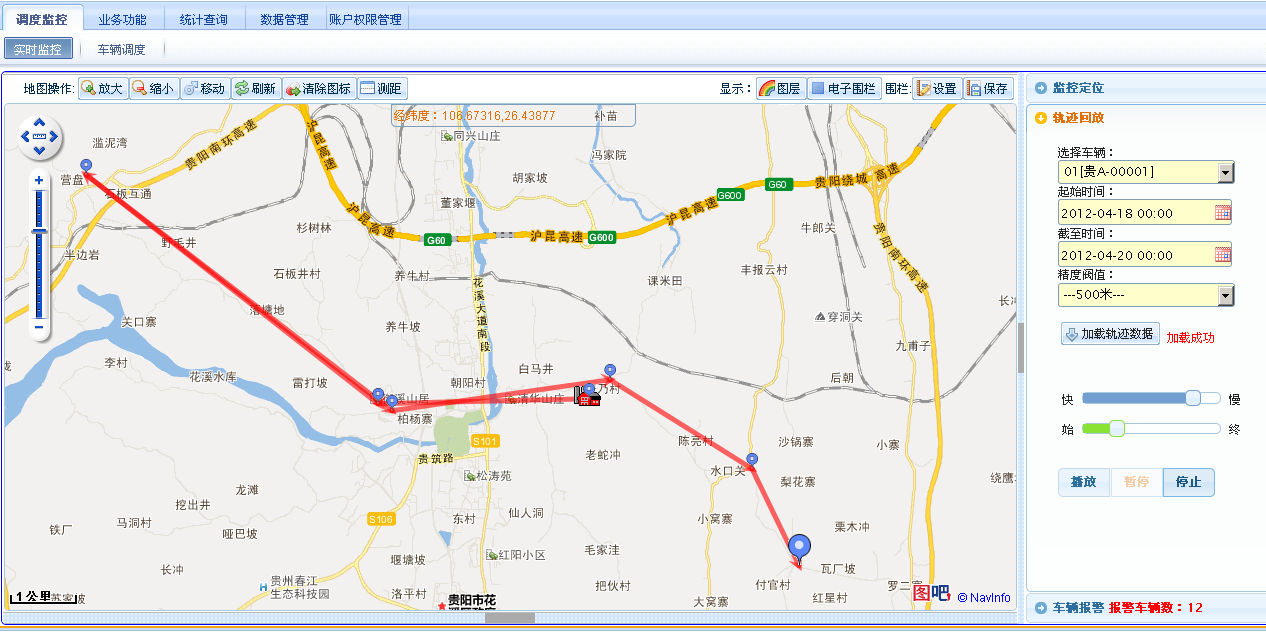
图三:2012年 中联搅拌车调度系统,贵阳某客户搅拌车 轨迹回放 ,500米阀值